- Handout No: 18 [Handout
berikutnya, sebelumnya, atau kembali ke
halaman
utama]
- dapat memiliki cabang berjumlah 0, 2, atau 3.
- Node-node leaf selalu berada pada level yang sama.
- key-key di cabang kiri < K1 < key-key di cabang kanan
- key-key di cabang kiri < K1 < key-key di cabang tengah
- key-key di cabang tengah < K1 < key-key di cabang kanan
- Mula-mula cari suatu leaf yang sesuai untuk menempatkan K tersebut. Masukanlah key tersebut pada node leaf tersebut. Kita sebut secara umum node ini sebagai P. Selanjutnya terdapat kasus-kasus pada P.
- P sebelumnya sebelumnya node-2 (berisi satu key) maka operasi selesai karena masih di dalam kapasitas node serta pula P kemudian menjadi node-3.
- P sebelumnya node-3, sekarang P kelebihan muatan dengan tiga key: K1, K2, dan K3 (K1 < K2 < K3), maka "pecah" node P (sebenarnya yang terjadi adalah, create satu node lainnya) menjadi dua node: P1 dan P2; jika P adalah internal node maka pemecahan menyertakan cabang-cabang disebelahnya
- P1 node di sebelah kiri ditempati oleh K1,
- P2 node di sebelah kanan ditempati oleh K3,
- sementara untuk K2 dilakukan:
- jika P bukan root maka K2 disisipkan ke node ayah dari P, dan pada ayah P di tambahkan satu pointer baru untuk menghubungkan ayah P dengan P1 dan P2.
- Jika P adalah root maka create node baru untuk menempatkan K2 yang kemudian menjadi root baru dan menghubungkan pointer kiri ke P1 dan pointer kanan ke P2.
- Ulangi prosedur pemeriksaan ini untuk ayah P sebagai P.
- Cari node yang berisikan key tersebut. Jika node ini bukan leaf maka cari node leaf yang berisikan key yang merupakan inorder predesesor dari K misalnya L dan memindahkan L tersebut ke tempat K semula sehingga masalahnya menjadi menghapus key dalam leaf. Untuk selanjutnya node leaf ini kita sebut P secara umum. P semula bisa merupakan node-2 atau node-3 sehingga sekarang menjadi bersisa satu key atau kosong.
- Jika P masih bersisa satu key maka proses selesai
- Jika tidak (P menjadi kosong) periksa lagi: jika P adalah root maka hapus node P, dan selesai (tentu saja jika P memiliki cabang maka node cabangnya menjadi root sekarang.
- jika tidak (bukan root) maka terdapat kasus-kasus yang masing-masing memerlukan operasi transformasi yang berbeda:
-
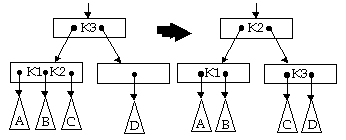
Kasus 1: P memiliki sibling tepat di kirinya yang memiliki 2 key.
Sibling tersebut adalah Q dan kedua key adalah K1 dan K2 (dimana
K1 < K2), maka apabila key yang memperantarainya di node ayah P adalah
K3 maka dilakukan rotasi:
K3 menempati P, K2 menggantikan K3, dan K1 tinggal sendirian di Q. Perpindahan
ini disertai oleh perpindahan subtree-subtree yang berkaitan dengan key
ybs.
-
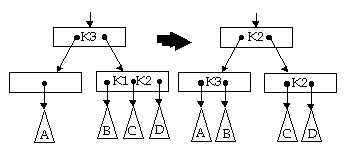
Kasus 2: P tidak memenuhi kasus 1,
tapi memiliki sibling tepat di kanannya yang memiliki 2 key
sibling tersebut adalah R dan kedua key adalah K1 dan K2 (di mana
K1 < K2). Apabila ada dan key K3 di ayah P memperantarai P dan R maka
dilakukan rotasi:
K3 menempati P, K1 menggantikan K3, dan K2 tinggal sendirian di R.
-
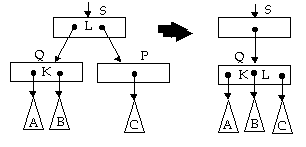
Kasus 3: P tidak memenuhi kasus 1 dan 2, tapi
memiliki sibling tepat dikirinya yang hanya memiliki 1 key.
Misalkan sibling tersebut adalah Q tersebut dan S adalah node
ayah dari P dan Q.
Pindahkan key yang memperantarai P dan Q dalam S ke Q sehingga kemudian
Q berisi dua key, serta P dapat di hapus berikut pointer pada S.
-
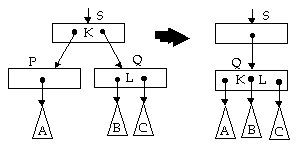
Kasus 4: P tidak memenuhi hasus 1, 2, dan 3, tapi
memiliki sibling tepat dikanannya yang hanya memiliki 1 key.
Misalkan sibling tersebut adalah Q tersebut dan S adalah node
ayah dari P dan Q.
Pindahkan key yang memperantarai P dan Q dalam S ke Q sehingga kemudian
Q berisi dua key, serta P dapat di hapus berikut pointer pada S.
 M/li>
M/li>
- Khusus pada kasus 3 atua 4, node S sekarang bisa menjadi kosong atau masih bersisa 1 key, maka jika S menjadi kosong lanjutkan proses dengan S sekarang sebagai P.
- Pada setiap path dari root ke leaf, jumlah edge hitam adalah sama
- Node merah yang bukan leaf selalu memiliki dua anak hitam.
- Suatu node hitam yang bukan merupakan leaf bisa memiliki:
- dua anak hitam;atau
- satu anak merah dan satu anak hitam; atau
- satu anak tunggal yang merah.
- setiap internal nodenya dapat memiliki a atau a+1 atau a+2 atau . . . atau b cabang serta (a < b)
- node leaf selalu berada pada level yang sama.
- Penyisipan terus berlangsung selama jumlah cabang lebih kecil atau sama dengan b. Manakala jumlah cabang mencapai b+1 maka node tersebut dipecah dua masing-masing membawa a cabang.
- Penghapusan terus dapat dilakukan pada suatu node selama jumlah cabang lebih besar atau sama dengan a. Kurang dari a maka dilakukan rotasi dari sibling node langsung yang berlebih atau jika tidak ada sibling langsung yang berlebih dilakukan penggabungan.
Struktur Data Hirarkis: 2-3 Tree dan B-Tree
7 April 1999
Disclaimer: pada tanggal 7 April 1999 page ini baru selesai 60% .... jadi jangan buru-buru diprint
Pengantar
AVL tree dalam pembahasan sebelumnya adalah salah satu suatu bentuk aplikasi tree sebagai tabel indeks. Alternatif struktur hirarkis lain untuk indexing adalah keluarga (a,b)-tree tree yang bukan binary tree. 2-3 Tree adalah versi yang paling sederhana dan B-Tree adalah versi yang paling populer digunakan dalam sistem basis data. Kelebihan struktur ini adalah dalam kestabilan performance pencarian logaritmisnya. Sebagaimana yang kita ketahui, AVL tree masih memungkinkan adanya perbedaan performance worse-case dan best-case.Definisi: suatu 2-3 tree adalah tree yang
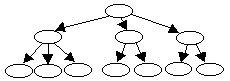
Dalam fungsinya sebagai suatu tabel indeks maka setiap node dapat berisi 2 key yaitu apabila memiliki 3 cabang atau merupakan leaf. Suatu node berisi 2 key disebut node-3 dan node dengan 1 key disebut node-2. Note: bilangan 2 dan 3 menunjukkan jumlah cabang yang ia miliki jika internal node, sebagai leaf maka penamaan tersebut tetap berlaku sesuai dengan jumlah key seolah leaf memiliki 2 atau 3 cabang kosong.
Keterurutan key pada Node-2 dengan key=K1:
Keterurutan pada Noe-3 dengan key K1 dan K2 (K1 < K2):
Dengan definisi demkian maka apabila setiap node dalam 2-3 tree
merupakan node-2 maka akan terbentuk perfect binary tree, sementara itu
apabila setiap node dalam 2-3 tree merupakan node-3 maka akan terbentuk
perfect ternary tree. Pada kedua bentuk perfect tree tersebut kedalaman
rata-rata dari tiap node adalah hampir sama dengan tinggi dari tree.
Pertanyaan: untuk jumlah node N berapa tinggi minimal dan maksimal dari 2-3 tree yang dapat terbentuk?
Penyisipan Suatu Key K
Dalam memahami proses penyisipan suatu key dalam 2-3 tree kita bayangkan node-node tree tersebut sebagai ruang-ruang yang elastis dengan kapasitas max 2 key dan apabila dimuati lebih dari kapasitas maka mula-mula key tersebut masuk tapi kemudian balon tsb. pecah.Penghapusan suatu Key K
Implementasi
Dengan bahasa pemrograman biasa maka implementasi node-2 dan node -3 memerlukan penanganan dengan algoritma yang berbeda. Beberapa bahasa pemrograman, menyediakan variant records (Pascal atau C), yaitu memungkinkan node-2 dan node-3 didekarasikan dalam satu block record dengan suatu variant flag. Namun dalam penanganannya tetap harus dibedakan. Selain itu, untuk kedua jenis node kompiler akan mengalokasikan space yang sama dengan mengambil space terbesarnya. Dalam bahasa pemrograman berorientasi obyek seperti C++ dan Java kedua node didefinisikan sebagai dua kelas yang berbeda dan merupakan subclass dari satu generic node class. Dalam hal ini algoritma manipulasinya bisa lebih disederhanakan karena sudah terdeferensiasi di dalam metoda-metodanya sendiri. Namun tentu saja sebagaimana umumnya konsep pemrograman berorientasi obyek, terdapat overhead cost yang lain untuk itu.Dalam Java spesifikasi dari node 2-3 tree.
- class TwoThreeTreeNode{
public void insertKey(KeyType x) {
}
}
class NodeTwo extends TwoThreeNode{
public void insertKey(KeyType x) {
}
}
class NodeThree extends TwoThreeNode {
public void insertKey(KeyType x) {
}
}
Sebagai suatu ADT maka 2-3 Tree dapat diimplementasikan dengan suatu
struktur Binary Search Tree yang memiliki sifat khusus yaitu Red-Black
Tree.
Red-Black Tree
Red-Black Tree adalah suatu BST yang mana node-node dan edge-edge memiliki warna merah atau hitam. Warna dari root selalu hitam. Warna dari edge yang menghubungkan ayah dengan anaknya selalu berwarna sama dengan warna node anak tersebut.Dalam merepresentasikan 2-3 Tree ke dalam Red-Black Tree maka diaplikasikan
aturan berikut. Jika setiap node-3 yang berisi key a dan b dan ketiga cabangnya
(t1, t2, dan t3) dipecahkan sbb.
atau
Selanjutnya hasil dari konversi 2-3 Tree menjadi Red-Black akan menghasilkan pewarnaan node dan edge dalam keteraturan sebagai berikut.
(a,b)-Tree
Generalisasi dari 2-3 Tree adalah (a,b)-tree yaitu suatu tree di mana
Aplikasinya berbeda dari 2-3 tree: Data hanya disimpan pada node
leaf sedangkan internal node pada (a,b)-tree hanya merupakan pembanding
mengarahkan pada node leaf yang sesuai. Jadi key-key dalam internal node
hanya dummy key (bisa duplikasi dengan real key) dan berfungsi sebagai
pengarah pada pencarian node leaf di mana data berada.
Penyisipan dan penghapusan data mirip dengan operasi penyisipan dan penghapusan pada 2-3 tree.
B-Tree
B-tree adalah (a,b)-tree di mana b = 2a - 1. a dan b biasanya merupakan angka-angka yang cukup besar, misalnya a = 100 dan b = 199.Hal tersebut berkaitan dengan fungsi B-tree untuk external data structure. Setiap node berukuran sesuai dengan ukuran data block. Misalnya terdapat satu juta item data yang disimpan pada external storage dan terbagi-bagi atas blok-blok. Sejumlah blok tambahan digunakan untuk menyimpan masing-masing internal node dan masing-masing interbal node dapat berisi 100 hingga 199 pointer. Retrieval suatu data paling buruk dilakukan dengan pembacaan 3 block internal node dan satu block node leaf yang berisi data yang dicari. Operasi block pada external storage biasa terjadi untuk mengurangi overhead cost untuk sistem mekanis alat baca pada pembacaan persatuan unit data.